5.5. Действия над векторами, заданными проекциями

Пусть векторы а=(a_x; a_y; a_z) и b=( b_x; b_y; b_z) заданы своими проекциями на оси координат Ox,Oy,Oz или, что то же самое

а = а_х •i + а_у • j +а_z • k,    b =b_х • i + b_у • j + b_z • k.

Линейные операции над векторами

Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:

1.          а ± b = (а_х ±b_х)i + (а_у ±b_y)j + ( a_z ± b_z)k, или кратко а ± b = (а_х ±b_x; a_y± b_y; a_z ± b_z). To есть при сложении (вычитании) векторових одноименные координаты складываются (вычитаются).

2.           l  а = l а_х • i + l а_у • j + l  a_z • k или короче l  а = (lа_х; lа_у; lа_z). То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

Равенство векторов

Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора а и b равны тогда и только тогда, когда выполняются равенства: a_х= b_х; а_у=b_y; a_z= b_z  , т. е.

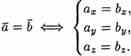
Коллинеарность векторов

Выясним условия коллинеарности векторов а и b, заданных своими координатами.

Так как а || b, то можно записать а = l • b, где l-некоторое число. То есть

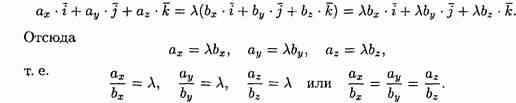
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.

Координаты точки

Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М координаты вектора ОМ называются координатами точки М. Вектор ОМ называется радиус-вектором точки

М, обозначается r , т. е. ОМ= r . Следовательно, координаты точки — это координаты ее радиус-вектора

 

Координаты точки М записываются в виде М(х; у; z ).

Координаты вектора Найдем координаты вектора а = АВ, если известны координаты точек A( x₁; y₁; z₁) и В( x₂;у₂; z₂). Имеем (см. рис. 13):

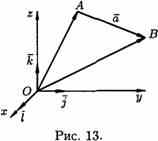        AB=OB-OA=(x₂i+y₂j+z₂k)-(x₁i+y₁j+z₁k)=(x₂ - x₁)i+(y₂ - y₁)j+(z₂ - z₁)k

Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала: АВ = (х₂-х₁;у₂-у₁; z₂- z₁).

6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

6.1. Определение скалярного произведения

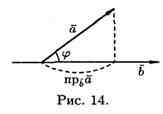
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

 

Формуле   (6.1)   можно   придать   иной   вид.   Так   как | a| cosg=пр _ba, (см. рис.14), a |b| cosg = пр _ab, то получаем:

     

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

6.2. Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

 

 << Пример 6.1

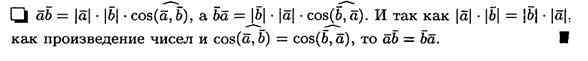
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b

.

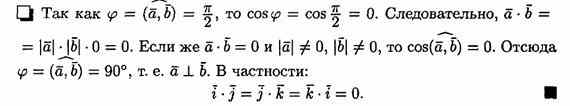
6.3. Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

  

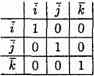
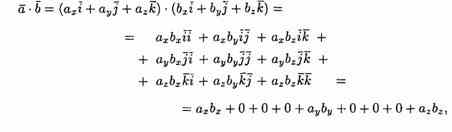
    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

<< Пример 6.2

6.4. Некоторые приложения скалярного произведения

Угол между векторами

    Определение угла φ между ненулевыми векторами а = (a_x; a_y; a_z) и b=( b_х; b_у; b_г):

Отсюда следует условие перпендикулярности ненулевых векторов а и b:

Проекция вектора на заданное направление

Нахождение проекции вектора а на направление, заданное вектором b, может осуществляться по формуле

Работа постоянной силы

Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы F, образующей угол j с перемещением АВ= S (см.рис. 15).

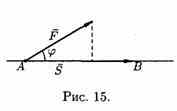
Из физики известно, что работа силы F при перемещении S равна

А=F•S•cosj   т. е.   А=(F•S).

Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

<< Пример 6.3

7. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

7.1. Определение векторного произведения

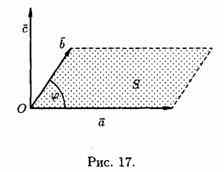
Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

     

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

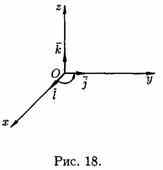
2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j.
Докажем, например, что iхj=k.

1) k^i, k^j;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

 

См. также

Оглавление |