Лекция № 9

7.5. Вычисление двойного интеграла в полярных координатах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.

Определим преобразование независимых переменных х и у (замену переменных) как

Если функции (7.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция ƒ(х;у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:

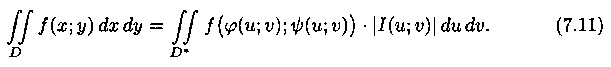
Функциональный определитель (7.10) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7.11) не приводим.Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и j.

В качестве u и υ возьмем полярные координаты r и j. Они связаны с декартовыми координатами формулами х=rcos j, у=r sin j (см. Часть 1, п. 9.1).

Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (7.10) как

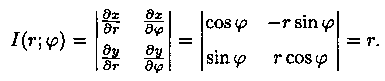
Формула замены переменных (7.11) принимает вид:

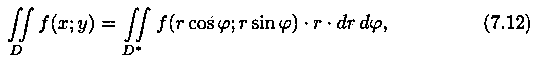
где D* - область в полярной системе координат, соответствующая области D в декартовой системе координат.

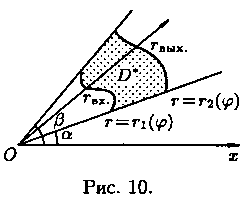Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область D* имеет вид, изображенный на рисунке 10 (ограничена лучами j=а и j=β, где а < β, и кривыми r=r₁(j) и r=r₂(j), где r₁(j)≤r₂(j), т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (7.12) можно  записать в виде

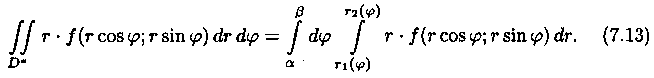
Внутренний интеграл берется при постоянном j.

Замечания.

1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ƒ(х²+у²); область D есть круг, кольцо или часть таковых.

2. На практике переход к полярным координатам осуществляется путем замены х=rcos j, у=rsin j, dxdy=r dr dj; уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по r и j (исследуя закон изменения r и j точки (r; j) при ее отождествлении с точкой (х; у) области D).

Пример 7.2. Вычислить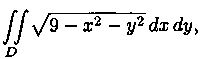где область D - круг

Решение: 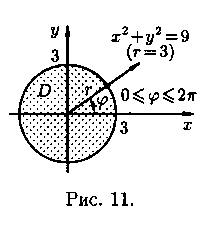Применив формулу (7.12), перейдем к полярным координатам:

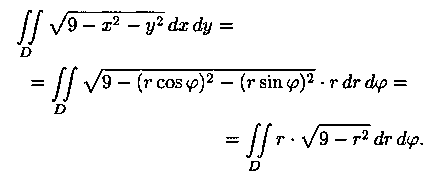
Область D в полярной системе координат определяется неравенствами (см. рис. 11) 0≤j≤2p,0≤r≤3. Заметим: область D - круг - преобразуется в область D* - прямоугольник. Поэтому, согласно формуле (7.13), имеем:

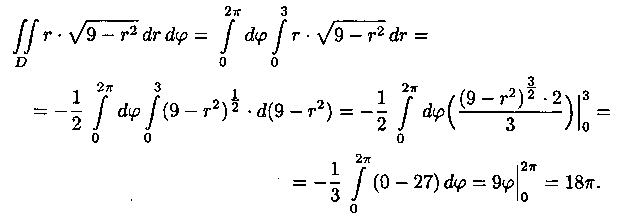
7.6. Приложения двойного интеграла

Приведем некоторые примеры применения двойного интеграла.

Объем тела

Как уже показано (п. 7.2), объем цилиндрического тела находится по формуле

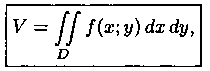
где z=ƒ(х;у) - уравнение поверхности, ограничивающей тело сверху.

Площадь плоской фигуры

Если положить в формуле (7.4) ƒ(х;у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н=1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

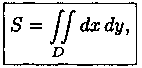
или, в полярных координатах,

Масса плоской фигуры

Как уже показано (п. 7.2), масса плоской пластинки D с переменной плотностью g=g(х;у) находится по формуле

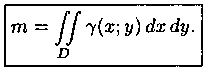
Статические моменты и координаты центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей Ох и Оу (см. Часть 1, п. 41.6) могут быть вычислены по формулам

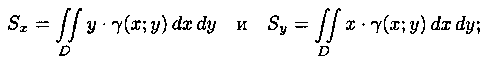
а координаты центра масс фигуры - по формулам

Моменты инерции плоской фигуры

Моментом инерции материальной точки массы м относительно оси l называется произведение массы м на квадрат расстояния d точки до оси, т. е. Мl=m • d². Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:

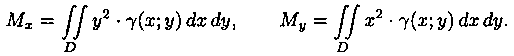
Момент инерции фигуры относительно начала координат - по формуле М_о=М_х +М_у.

Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 11.3).

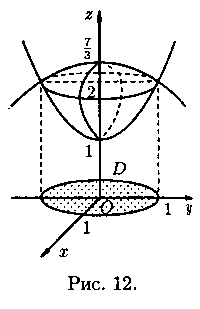
Пример 7.3. Найти объем тела, ограниченного поверхностями х²+у²-z+1=0 и x²+y²+3z-7=0.

Решение: Данное тело ограничено двумя параболоидами (см. рис. 12). Решая систему

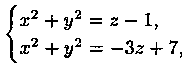
находим уравнение линии их пересечения: х²+у²=1, z=2.

Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг х²+у²≤1) и ограниченных сверху соответственно поверхностями

Используя формулу (7.4), имеем

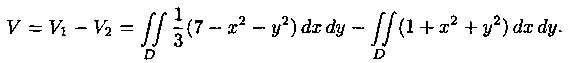
Переходя к полярным координатам, находим:

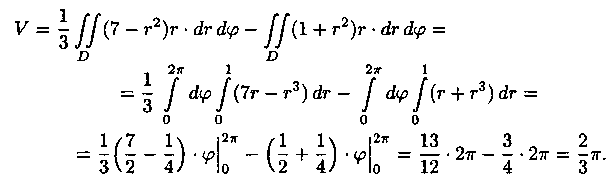
Пример 7.4.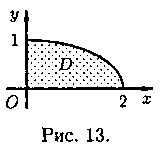 Найти массу, статические моменты S_x и S_y и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями (см. рис. 13). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение: По формуле (7.6) находим массу пластинки. По условию, g=g(х;у)= k • ху, где k - коэффициент пропорциональности.

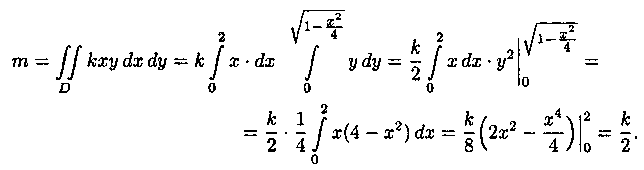
Находим статические моменты пластинки:

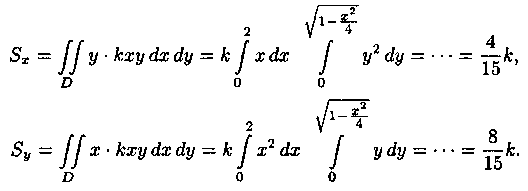
Находимкоординаты центра тяжести пластинки, используя формулы

§8. ТРОЙНОЙ ИНТЕГРАЛ

8.1. Основные понятия

Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».

Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.Пусть в замкнутой области V пространства Oxyz задана непрерывная функция u=ƒ(х;у;z). Разбив область V сеткой поверхностей на n частей и выбрав в каждой из них произвольную точку М_i(х_i;y_i;z_i), составим интегральную суммудля функции ƒ(х; у; z) по

области V (здесь ∆V_i - объемэлементарной области V_i).

Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая «элементарная область» Vi стягивается в точку (т. е. диаметр области d_i стремится к нулю, т. е. di-> 0), то его называют тройным интегралом от функции u=ƒ(х;у;z) по области V и обозначают

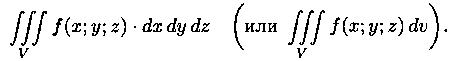
Таким образом, по определению, имеем:

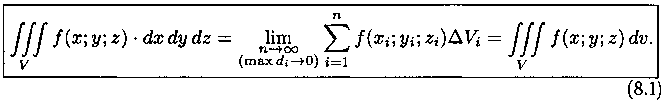
Здесь dv=dx dy dz - элемент объема.

Тройной интеграл обладает теми же свойствами, что и двойной интеграл:

1.

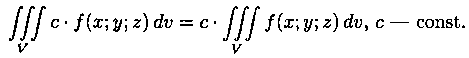
2.

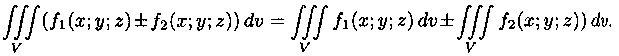
3. 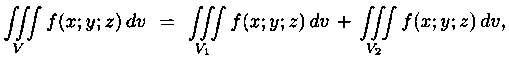если V=V₁ È V_2, а пересечение V₁ и V₂ состоит из границы, их разделяющей.

4. 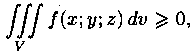если в области V функция f(x;y;z)>=0. Если в области интегрирования ƒ(х;у;z)>=j(x;y;z), то и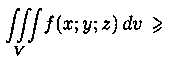

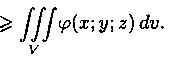
5 .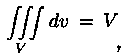, так как в случаелюбая интегральная сумма имеет вид и численно равна объему тела.

6. Оценка тройного интеграла:

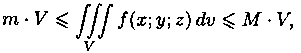
где m и М - соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.

7. Теорема о среднем значении: если функция f(x;y;z) непрерывна в замкнутой области V, то в этой области существует такая точка M_o(x_o;y_o;z_o), что

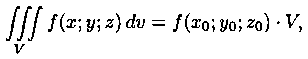
где V - объем тела.

См. также

Оглавление |