Глава II. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ

§7. ДВОЙНОЙ ИНТЕГРАЛ

7.1. Основные понятия и определения

Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Оху задана непрерывная функция z=ƒ(х;у). Разобьем область D на n «элементарных областей»  площади которых обозначим через ΔS_i, а диаметры (наи большее расстояние между точками области) - через d_i(см. рис. 3).

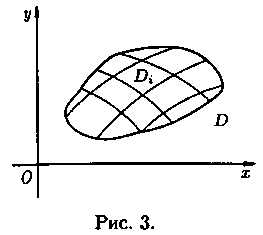В каждой области D_i выберем произвольную точку M_i(x_i;y_i), умножим значение ƒ(х_i;у_i) функции в этой точке на ΔS_i и составим сумму всех таких произведений:

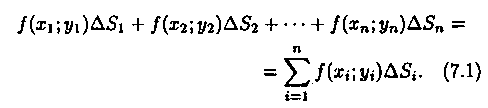
 Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.

Рассмотрим предел интегральной суммы (7.1), когда n стремится к бесконечности таким образом, что maxd_i -> 0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается

Таким образом, двойной интеграл определяется равенством

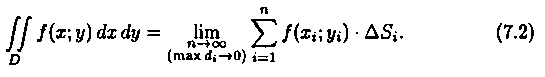
В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.

Для всякой ли функции ƒ(х;у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.

Замечания.

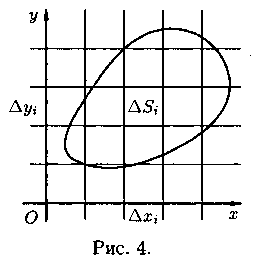1. Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.

2. Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллель ными координатным осям (см. рис. 4). При этом равенство (7.2) можно записать в виде

7.2. Геометрический и физический смысл двойного интеграла

Рассмотрим две задачи, приводящие к двойному интегралу.

Объем цилиндрического тела

Рассмотрим тело, ограниченное сверху поверхностью снизу - замкнутой  областью D плоскости Оху, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 5). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=ƒ(х;у) на плоскость Оху) произвольным образом на п областей Di, площади которых равны Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z=ƒ(х;у)  (на рис. 5 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием D_i через ∆V_i, получим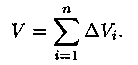

Возьмем на каждой площадке D_i произвольную точку  M_i(x_i;,y_i) и заменим каждый столбик прямым цилиндром с тем же основанием D; и высотой z_i=ƒ(х_i;у_i).

Объем этого цилиндра приближенно равен объему ΔV_i цилиндрического

столбика, т. е.. Тогда получаем:

 

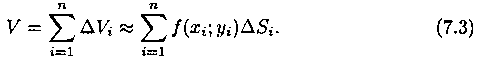
Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» D_i. Естественно принять предел суммы (7.3) при условии, что число площадок D_i неограниченно увеличивается (n -> ∞), а каждая площадка стягивается в точку (maxd_i-> 0), за объем V цилиндрического тела, т. е.

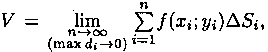
или, согласно равенству (7.2),

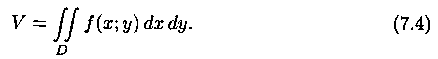
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.

Масса плоской пластинки

Требуется найти массу m плоской пластинки D, зная, что ее поверхностная плотность g=g(х;у) есть непрерывная функция координат точки (х;у). Разобьем пластинку D на п элементарных частей площади которых обозначим через ∆S_i. В каждой области D; возьмем произвольную точку М_i(х_i;у_i) и вычислим плотность в ней:

Если области D_i достаточно малы, то плотность в каждой точке (х;у) є D_i мало отличается от значения g(x_i;y_i). Считая приближенно плотность в каждой точке области D_i постоянной, равной g(x_i;y_i), можно найти ее массу Так как масса m всей пластинки D равна то для ее  вычисления имеем приближенное равенство

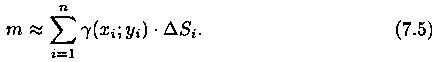
Точное значение массы получим как предел суммы (7.5) при условии n ->∞ и max d_i -> 0:

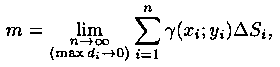
или, согласно равенству (7.2),

Итак, двойной интеграл от функции g(x;у) численно равен массе пластинки, если подынтегральную функцию g(х;у) считать плотностью этой пластинки в точке (х;у). В этом состоит физический смысл двойного интеграла.

7.3. Основные свойства двойного интеграла

Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. Часть 1, п. 35). Аналогичны и свойства этих интегралов и их доказательства. Поэтому перечислимосновные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.

1.

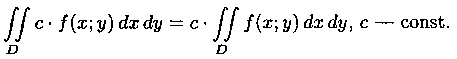
2.

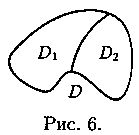3. Если область D разбить линией на две област и D1 и D2 такие, чтоа пересечение D1 и D состоит лишь из линии, их разделяющей (см. рис. 6), то

4.Если в области D имеет место неравенство ƒ(х;у) >=0, то и Если в области D функции ƒ(х; у) и j(х; у) удовлетворяютнеравенству

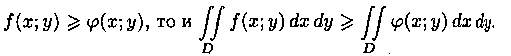
5.

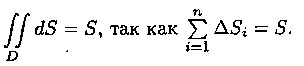
6. Если функция ƒ(х; у) непрерывна в замкнутой области D, площадь которой S, то 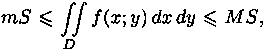где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.

7. Если функция ƒ(х;у) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (х_о;у_о), что

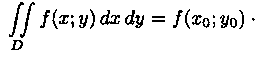S.

Величину называют средним значением функции ƒ(х;у) в области D.

7.4. Вычисление двойного интеграла в декартовых координатах

Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

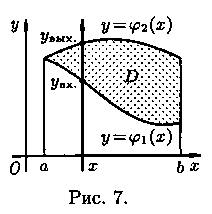Пусть требуется вычислить двойной интеграл где функция ƒ(х;у)>=0 непрерывна в области D. Тогда, как это было показано в п. 7.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z=ƒ(х;у). Найдем этот объем, используя метод параллельных сечений. Ранее (см. Часть 1, (41.6)) было показано, что

где S(x) - площадь сечения плоскостью, перпендикулярной оси Ох, a x=a,x=b - уравнения плоскостей, ограничивающих данное тело.

Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=j₁(x) и у=j₂(х), причем функции j₁(x) и j₂(х) непрерывны и таковы, что j₁(x) ≤ j₂(х) для всех х є [а;b] (см. рис. 7). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.

Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х =const, где х є [а; b].

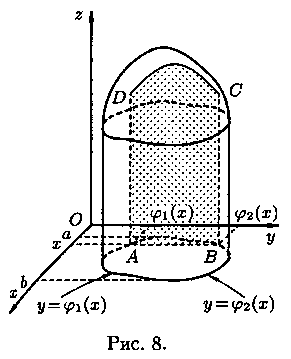
В сечении получим криволинейную трапецию ABCD, ограниченную линиями z=ƒ(х;у), где х=const, z=0, у=j₁(x) и у=j₂(х) (см. рис. 8). Площадь S(х) этой трапеции находим с помощью определенного интеграла

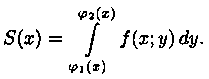
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть  найдентак:

С другой стороны, в п. 7.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции ƒ(х;у) >=0 по области D. Следовательно,

Это равенство обычно записывается в виде

Формула (7.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (7.7) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.

При этом   называется внутренним интегралом.

Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.

Если же область D ограничена прямыми y=c и y=d(c<d), кривыми x=Ψ₁(у)и х=Ψ₂(у)> причем Ψ₁(у)≤Ψ₂(у) для всех у є [с;d], т. е. область D - правильная в направлении оси Ох, то, рассекая тело плоскостью у=const, аналогично получим:

Здесь, при вычислении внутреннего интеграла, считаем у постоянным.

Замечания.

1. Формулы (7.7) и (7.8) справедливы и в случае, когда ƒ(х;у)<0, (x;y) e D.

2. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (7.7), так и по формуле (7.8).

3. Если область D не является правильной ни «по х», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.

4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.

 

Пример 7.1. 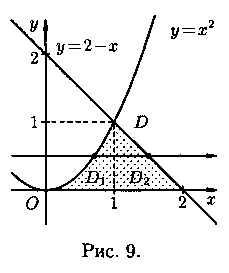Вычислить 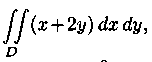где область D ограничена линиями у =x², у=0, х+у-2=0.

Решение: На рисунке 9 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (7.8):

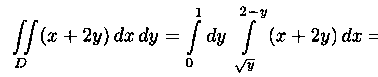
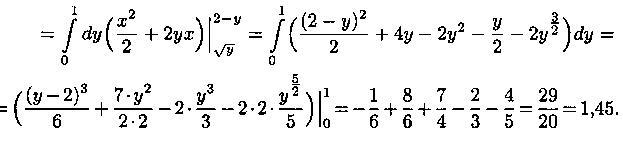
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (7.7). Но для этого область D следует разбить на две области: D₁ и D₂. Получаем:

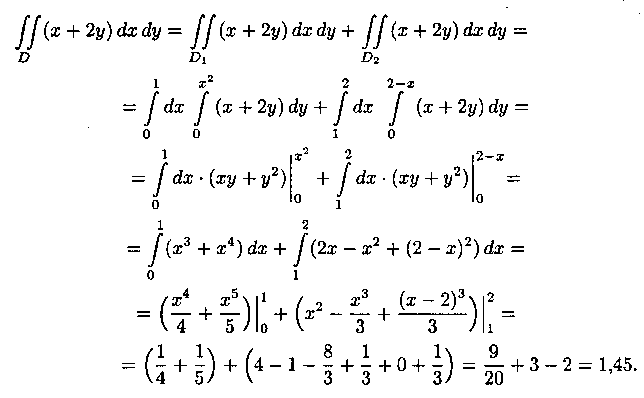
Ответ, разумеется, один и тот же.

См. также

Оглавление |