2.3. однородные дифференциальные уравнения

К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.

Функция ƒ(x;y) называется однородной функцией N-го поpядкa (измерения), если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на A^N, т. е.

Например, функция ƒ(x;у)=х²-2ху есть однородная функция вто-рого порядка, поскольку

Дифференциальное уравнение

У'=ƒ(х; у)         (2.7)

называется однородным, если функция ƒ(х;у) есть однородная функция нулевого порядка.

Покажем, что однородное ДУ (2.7) можно записать в виде

Если ƒ(x;у) - однородная функция нулевого порядка, то, по определению, Положив получаем:

однородное уравнение (2.8) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки)

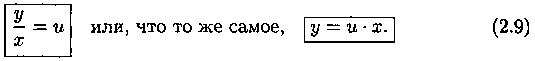
Действительно, подставив у=uх и y^'=u'x+u в уравнение (2.8), получаем уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем u на . Получим общее решение (интеграл) исходного уравнения.

Однородное уравнение часто задается в дифференциальной форме:

ДУ (2.10) будет однородным, если Р(х;у) и Q(x;у) - однородные функции одинакового порядка.

Переписав уравнение (2.10) в видеи применив в правой части рассмотренное выше преобразование, получим уравнение

При интегрировании уравнений вида (2.10) нет необходимости предварительно приводить их (но можно) к виду (2.8): подстановка (2.9) сразу преобразует уравнение (2.10) в уравнение с разделяющимися переменными.

Пример 2.6. Найти общий интеграл уравнения

Решение: Данное уравнение однородное, т. к. функции Р(х;у)=х²-у² и Q(x;у)=2ху - однородные функции второго порядка.

Положим у=u • х. Тогда dy=х • du+u • dx. Подставляем в исходное уравнение:

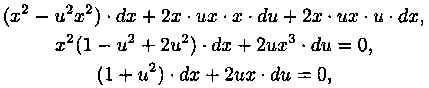
последнее - уравнение с разделяющимися переменными. Делим переменные

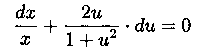
и интегрируем

Обозначим Тогда

Заменяя u наполучаем: х²+у²=сх - общий интеграл исходного уравнения.

Отметим, что данное уравнение можно было сначала привести к виду (2.8):

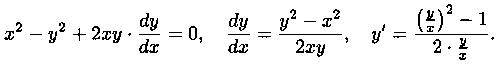
Затем положить у=u • х, тогда y^'=u'x+u и т. д.

Замечание. Уравнение вида где а, b, с, a₁, b₁, c1 - числа, приводится к однородному или с разделяющимися переменными. Для этого вводят новые переменные u и v, положив х=u+а, y=v+β, где а и β - числа. Их подбирают так, чтобы уравнение стало однородным.

 

Пример 2.7. Найти общий интеграл уравнения

т. е.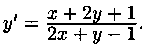

Решение: Положивполучаем:

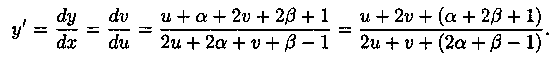
Подберем а и β так, чтобы

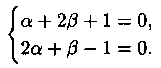
Находим, что а=1, β=- 1. Заданное уравнение примет вид

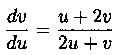
и будет являться однородным. Его решение получается, как это было показано выше, при помощи подстановки v=tu. Заметим, что, решив его, следует заменить u и v соответственно на х-1 и y+1. В итоге получим (y-х+2)³=с(х+у) - общий интеграл данного уравнения.

2.4. Линейные уравнения. Уравнение Я. Бернулли

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде

где р(х) и g(x) - заданные функции, в частности - постоянные.

Особенность ДУ (2.11): искомая функция у и ее производная y' входят в уравнение в первой степени, не перемножаясь между собой.

Рассмотрим два метода интегрирования ДУ (2.11) - метод И. Бернулли и метод Лагранжа.

Метод И. Бернулли

Решение уравнения (2.11) ищется в виде произведения двух других функций, т. е. с помощью подстановки y=u • v, где u=u(x) и v=v(x) - неизвестные функции от х, причем одна из них произвольна (но не равна нулю - действительно любую функцию y(х) можно записать как

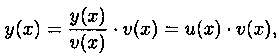
где v(x) ≠ 0). Тогда y'=u'•v+u•v'. Подставляя выражения y и y' в уравнение (2.11), получаем: u' • v+u • v'+р(х) • u • v=g(x) или

Подберем функцию v=v(x) так, чтобы выражение в скобках было равно нулю, т. е. решим ДУ v^'+р(х) • v=0. Итак,т. е. Интегрируя, получаем:

Ввиду свободы выбора функции v(x), можно принять с=1. Отсюда

Подставляя найденную функцию v в уравнение (2.12), получаем

Получено уравнение с разделяющимися переменными. Решаем его:

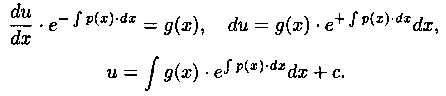
Возвращаясь к переменной υ, получаем решение

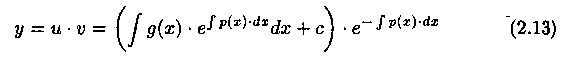
Пример 2.8. Проинтегрировать уравнение y^'+2xy=2х.

Решение: Полагаем у=u•v. Тогда u^' * v+u • v'+2х ' uv=2х, т. е. u' • v+u•(v'+2xv)=2х. Сначала решаем уравнение v'+2х • v=0:

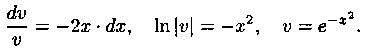
Теперь решаем уравнение

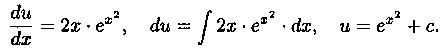
Итак, общее решение данного уравнения есть т. е.

Метод Лагранжа (метод вариации произвольной постоянной)

Уравнение (2.11) интегрируется следующим образом.

Рассмотрим соответствующее уравнение без правой части, т. е. уравнение y' +р(х) • y=0. Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся:

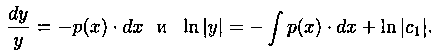
Таким образом,

Метод вариации произвольной постоянной состоит в том, что постоянную с в полученном решении заменяем функцией с(х), т. е. полагаем с=с(х). Рєшение уравнения (2.11) ищем в виде

Находим производную^:

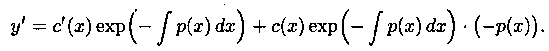
Подставляем значения у и у^' в уравнение (2.11):

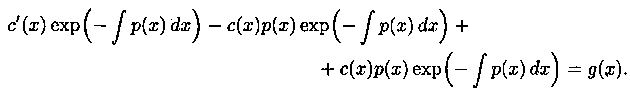
Второе и третье слагаемые взаимно уничтожаются, и уравнение примет вид

Следовательно,

Интегрируя, находим:

Подставляя выражение с(х) в равенство (2.14), получим общее решение ДУ (2.11):

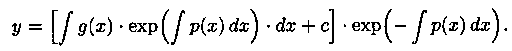
Естественно, та же формула была получена методом Бернулли (ср. с (2.13)).

 

Пример 2.9. Решить пример 2.8 методом Лагранжа.

Решение: Решаем уравнениеИмеем или . Заменяем с на с(х), т. е. решение ДУ у^'+2ху=2х ищем в виде . Имеем

Тогда

илиили

Поэтому или - общее решение данного уравнения.

 

Замечание. Уравнение вида

- заданные функции, можно свести к линейному, если х считать функцией, а y - аргументом: х=х(у). Тогда, пользуясь равенством

получаем

 линейное относительно х уравнение. Его решение ищем в виде х=u•v, где u=u(y), v=v(y) - две неизвестные функции.

 

Пример 2.10. Найти общее решение уравнения (х+υ)•y'=1.

Решение: Учитывая, чтоот исходного уравнения переходим к линейному уравнению x^'=х+y.

Применим подстановку х=u • v. ТогдаПолучаем:

или

Находим функцию v:

Находим функцию u:

Интегрируя по частям, находим: u=-y • е^-у - е^-у+с. Значит, общее решение данного уравнения: или

Уравнение Я. Бернулли

Уравнение вида

называется уравнением Бернулли. Покажем, что его можно привести к линейному.

Если n=0, то ДУ (2.15) - линейное, а при n=1 - с разделяющимися переменными.

В общем случае, разделив уравнение (2.15) на yⁿ ≠ 0, получим:

ОбозначимТогдаОтсюда находим

Уравнение(2.16) принимает вид

Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка z=y^-n+1 сводит уравнение (2.15) к линейному. На практике ДУ (2.15) удобнее искать методом И. Бернулли в виде υ=u•v (не сводя его к линейному).

См. также

Оглавление |