Ссылки
Уравнения прямой на
плоскости
Прямая линия на плоскости. Основные задачи.
§ 11 Линии второго порядка на плоскости
Основные понятия
Окружность
Эллипс
10.2. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды её уравнений.
Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N(0; b) пересечения с осью Оу и углом a между осью Ох и прямой (см. рис. 41).
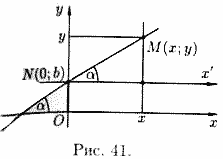
Под углом а (0<a< p) наклона прямой понимается наименьший угол, на который нужно повернуть вокруг точки пересечения прямой и оси Ох против часовой стрелки ось Ох до ее совпадения с прямой. Возьмем на прямой произвольную точку М(х;у) (см. рис. 41). Проведем через точку N ось Nx', параллельную оси Ох и одинаково с ней направленную. Угол между осью Nx' и прямой равен a. В системе Nx'y точка Μ имеет координаты x и у-b.
Из определения тангенса угла следует равенство
![]() ,
т. е.
,
т. е. ![]() .
.
Введем обозначение tg a=k, получаем уравнение
![]() (10.2)
(10.2)
которому удовлетворяют координаты любой точки М(х;у) прямой. Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (10.2) не удовлетворяют.
Число k = tga называется угловым коэффициентом прямой, а уравнение (10.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид y=kx.
Если прямая параллельна оси Ох, то a = 0, следовательно, k = tga = 0 и уравнение (10.2) примет вид у = b.
Если прямая параллельна оси Оу, то
![]() ,
уравнение (10.2) теряет смысл, т. к. для нее угловой коэффициент
,
уравнение (10.2) теряет смысл, т. к. для нее угловой коэффициент
![]() не
существует.
не
существует.
В этом случае уравнение прямой будет иметь вид
![]() (10.3)
(10.3)
где a — абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (10.2) и (10.3) есть уравнения первой степени.
Общее уравнение прямой.
Рассмотрим уравнение первой степени относительно x и y в общем виде
![]() (10.4)
(10.4)
где А, В, С — произвольные числа, причем А и В не равны нулю одновременно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.
Если В = 0, то уравнение (10.4) имеет вид Ах + С = О, причем А ¹
0 т. е.
![]() .
Это есть уравнение прямой, параллельной оси Оу и проходящей через точку
.
Это есть уравнение прямой, параллельной оси Оу и проходящей через точку
![]() ·
·
Если B ¹ 0, то из уравнения (10.4) получаем
![]() .
Это есть уравнение прямой с угловым коэффициентом
.
Это есть уравнение прямой с угловым коэффициентом
![]() |.
|.
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
1) если А = 0, то уравнение приводится к виду![]() .
Это есть уравнение прямой, параллельной оси Ох;
.
Это есть уравнение прямой, параллельной оси Ох;
2) если В = 0, то прямая параллельна оси Оу;
3) если С = 0, то получаем
![]() . Уравнению
удовлетворяют координаты точки O(0;0), прямая проходит через начало
координат.
. Уравнению
удовлетворяют координаты точки O(0;0), прямая проходит через начало
координат.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку
![]() и ее направление
определяется угловым коэффициентом k. Уравнение этой прямой можно
записать в виде
и ее направление
определяется угловым коэффициентом k. Уравнение этой прямой можно
записать в виде ![]() ,
где b — пока неизвестная величина. Так как прямая проходит через точку
,
где b — пока неизвестная величина. Так как прямая проходит через точку
![]() , то координаты
точки удовлетворяют уравнению прямой:
, то координаты
точки удовлетворяют уравнению прямой:![]() .
Отсюда
.
Отсюда ![]() .
Подставляя значение b в уравнение
.
Подставляя значение b в уравнение![]() ,
получим искомое уравнение прямой:
,
получим искомое уравнение прямой:
![]() , т. е.
, т. е.
![]() (10.5)
(10.5)
Уравнение (10.5) с различными значениями k называют также уравнениями пучка
прямых с центром в точке![]() Из
этого пучка нельзя определить лишь прямую, параллельную оси Оу.
Из
этого пучка нельзя определить лишь прямую, параллельную оси Оу.
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки
![]() и
и
![]() . Уравнения
прямой, проходящей через точку M1, имеет вид
. Уравнения
прямой, проходящей через точку M1, имеет вид
![]()
![]() (10.6)
(10.6)
где k — пока неизвестный коэффициент.
Так как прямая проходит через точку
![]() , то координаты
этой точки должны удовлетворять уравнению (10.6):
, то координаты
этой точки должны удовлетворять уравнению (10.6):
![]() . Οтсюда находим
. Οтсюда находим
![]() .
Подставляя найденное значение k в уравнение (10.6), получим уравнение
прямой, проходящей через точки M1
и M2.
.
Подставляя найденное значение k в уравнение (10.6), получим уравнение
прямой, проходящей через точки M1
и M2.
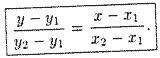 (10.7)
(10.7)
Предполагается, что в этом уравнении
![]() ·
·
Если x2 = x1 прямая, проходящая через точки
![]() и
и
![]() параллельна оси
ординат. Ее уравнение имеет вид
параллельна оси
ординат. Ее уравнение имеет вид
![]() .
.
Если y2 = y1 то уравнение прямой может быть записано в
виде ![]() , прямая M1M2
параллельна оси абсцисс.
, прямая M1M2
параллельна оси абсцисс.
Уравнение прямой в отрезках
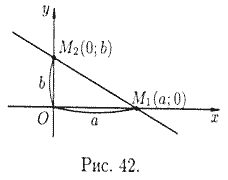 Пусть
прямая пересекает ось Ох в точке
Пусть
прямая пересекает ось Ох в точке
![]() , а ось Оу – в
точке
, а ось Оу – в
точке ![]() (см. рис.
42). В этом случае уравнение (10.7) примет вид
(см. рис.
42). В этом случае уравнение (10.7) примет вид
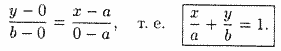
Это уравнение называется уравнением прямой в отрезках, так как числа α и b указывают, какие отрезки отсекает прямая на осях координат.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой, проходящей
через заданную точку
![]() перпендикулярно
данному ненулевому вектору
перпендикулярно
данному ненулевому вектору
![]() .
.
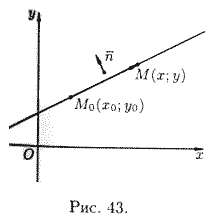 Возьмем
на прямой произвольную точку М(х;у) и рассмотрим вектор
Возьмем
на прямой произвольную точку М(х;у) и рассмотрим вектор
![]() (см. рис. 43).
Поскольку векторы
(см. рис. 43).
Поскольку векторы ![]() и
и
![]() перпендикулярны,
то их скалярное произведение равно нулю:
перпендикулярны,
то их скалярное произведение равно нулю:
![]() , то есть
, то есть
![]()
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор ![]() ,
перпендикулярный прямой, называется нормальным вектором этой прямой. Уравнение
(10.8) можно переписать в виде
,
перпендикулярный прямой, называется нормальным вектором этой прямой. Уравнение
(10.8) можно переписать в виде
![]() (10.9)
(10.9)
где А и B— координаты нормального вектора,
![]() — свободный член.
Уравнение (10.9) есть общее уравнение прямой (см. (10.4)).
— свободный член.
Уравнение (10.9) есть общее уравнение прямой (см. (10.4)).
Полярное уравнение прямой
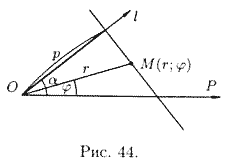 Найдем
уравнение прямой в полярных координатах. Ее положение можно определить, указав
расстояние ρ от полюса О до данной прямой и угол α между полярной осью ОΡ и
осью l, проходящей через полюс О перпендикулярно данной прямой (см. рис.
44).
Найдем
уравнение прямой в полярных координатах. Ее положение можно определить, указав
расстояние ρ от полюса О до данной прямой и угол α между полярной осью ОΡ и
осью l, проходящей через полюс О перпендикулярно данной прямой (см. рис.
44).
Для любой точки
![]() на
данной прямой имеем:
на
данной прямой имеем:
![]()
С другой стороны,
![]()
Следовательно,
![]() (10.10)
(10.10)
Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
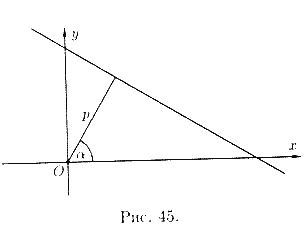
Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см.
рис. 45). Рассмотрим прямоугольную систему координат
![]() . Введем полярную
систему, взяв
. Введем полярную
систему, взяв ![]() за
полюс и
за
полюс и ![]() за
полярную ось. Уравнение прямой можно записать в виде
за
полярную ось. Уравнение прямой можно записать в виде
![]() ,
т. е.
,
т. е. ![]() .
.
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем:
![]() ,
,
![]() . Следовательно,
уравнение (10.10) прямой в прямоугольной системе координат примет вид
. Следовательно,
уравнение (10.10) прямой в прямоугольной системе координат примет вид
![]() (10.11)
(10.11)
Уравнение (10.11) называется нормальным уравнением прямой.
 Покажем,
как привести уравнение (10.4) прямой к виду
(10.11).
Покажем,
как привести уравнение (10.4) прямой к виду
(10.11).
Умножим все члены уравнения (10.4) на некоторый множитель
![]() . Получим
. Получим
![]() . Это уравнение
должно обратиться в уравнение (10.11). Следовательно, должны выполняться
равенства:
. Это уравнение
должно обратиться в уравнение (10.11). Следовательно, должны выполняться
равенства: ![]() ,
,
![]() ,
,
![]() . Из первых двух
равенств находим
. Из первых двух
равенств находим![]() ,т.
е.
,т.
е. ![]() .
Множитель λ называется нормирующим множителем. Согласно третьему
равенству
.
Множитель λ называется нормирующим множителем. Согласно третьему
равенству ![]() знак
нормирующего множителя противоположен знаку свободного члена С общего
уравнения прямой.
знак
нормирующего множителя противоположен знаку свободного члена С общего
уравнения прямой.
10.3 Прямая линия на плоскости. Основные задачи
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые L1 и L2
заданы уравнениями с угловыми коэффициентами
![]() и
и
![]() (см. рис. 46).
(см. рис. 46).
Требуется найти угол φ, на который надо повернуть в положительное направлении прямую L1 вокруг точки их пересечения до совпадения с прямой L2.
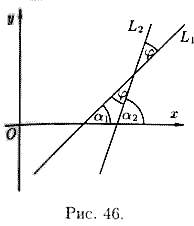 Решение:
Имеем
Решение:
Имеем ![]() (теорема о
внешнем угле треугольника) или
(теорема о
внешнем угле треугольника) или
![]() . Если
. Если
![]() , то
, то
![]()
Но ![]() ,
,
![]() , поэтому
, поэтому
 (10.12)
(10.12)
откуда легко получим величину искомого угла.
Если требуется вычислить острый угол между
прямыми, не учитывая, какая прямая является первой, какая — второй, то правая
часть формулы (10.12) берется по модулю, т. е.
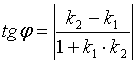
Если прямые L1 и L2
параллельны, то φ = 0 и
![]() . Из формулы
(10.12) следует
. Из формулы
(10.12) следует ![]() ,
т. е.
,
т. е. ![]() . И обратно,
если прямые L1 и L2 таковы, что
. И обратно,
если прямые L1 и L2 таковы, что
![]() , то
, то
![]() , т. е. прямые
параллельны. Следовательно, условием параллельности двух прямых является
равенство их угловых коэффициентов:
, т. е. прямые
параллельны. Следовательно, условием параллельности двух прямых является
равенство их угловых коэффициентов:
![]() .
.
Если прямые L1 и L2
перпендикулярны, то
![]() .
Следовательно,
.
Следовательно,
![]() .
Отсюда
.
Отсюда ![]() , т. е.
(или
, т. е.
(или
![]() ).
Справедливо и обратное утверждение. Таким образом, условием перпендикулярности
прямых является равенство
).
Справедливо и обратное утверждение. Таким образом, условием перпендикулярности
прямых является равенство
![]() .
.
Расстояние от точки до прямой
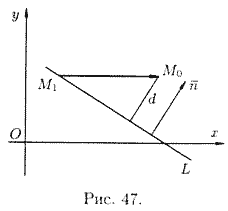 Пусть
заданы прямая L уравнением
Пусть
заданы прямая L уравнением
![]() и точка
и точка
![]() (см. рис. 47).
Требуется найти расстояние от точки
(см. рис. 47).
Требуется найти расстояние от точки
![]() до
прямой L.
до
прямой L.
Решение : Расстояние d отточки![]() до
прямой L равно модулю проекции вектора
до
прямой L равно модулю проекции вектора
![]() , где
, где
![]() - произвольная
точка прямой L, на направлении
нормального
- произвольная
точка прямой L, на направлении
нормального
вектора
![]() .
Следовательно,
.
Следовательно,
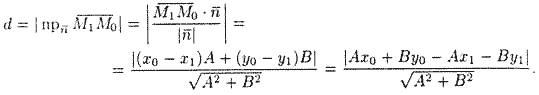
Так как точка ![]() принадлежит
прямой L, то
принадлежит
прямой L, то
![]() , т. е.
, т. е.
![]() . Поэтому
. Поэтому
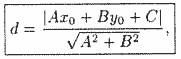 (10.13)
(10.13)
что и требовалось получить.
§11. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
![]() (11.1)
(11.1)
Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11.1) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.
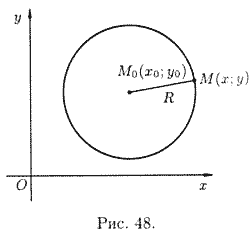 Простейшей
кривой второго порядка является окружность. Напомним, что окружностью радиуса R
с центром в точке
Простейшей
кривой второго порядка является окружность. Напомним, что окружностью радиуса R
с центром в точке ![]() называется
множество всех точек Μ плоскости, удовлетворяющих условию
называется
множество всех точек Μ плоскости, удовлетворяющих условию
![]() . Пусть точка
. Пусть точка
![]() в прямоугольной
системе координат
в прямоугольной
системе координат ![]() имеет
координаты x0, y0 а
имеет
координаты x0, y0 а
![]() — произвольная
точка окружности (см. рис. 48).
— произвольная
точка окружности (см. рис. 48).
Тогда из условия
![]() получаем
уравнение
получаем
уравнение
![]() , то есть
, то есть
![]() (11.2)
(11.2)
Уравнению (11.2) удовлетворяют координаты любой точки
![]() данной окружности
и не удовлетворяют координаты никакой точки, не лежащей на окружности.
данной окружности
и не удовлетворяют координаты никакой точки, не лежащей на окружности.
Уравнение (11.2) называется каноническим уравнением окружности
В частности, полагая
![]() и
и
![]() , получим
уравнение окружности с центром в начале координат
, получим
уравнение окружности с центром в начале координат
![]() .
.
Уравнение окружности (11.2) после несложных преобразований примет вид
![]() . При сравнении
этого уравнения с общим уравнением (11.1) кривой второго порядка легко
заметить, что для уравнения окружности выполнены два условия:
. При сравнении
этого уравнения с общим уравнением (11.1) кривой второго порядка легко
заметить, что для уравнения окружности выполнены два условия:
1) коэффициенты при x2 и у2 равны между собой;
2) отсутствует член, содержащий произведение xу текущих координат.
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения
![]() и
и
![]() , получим
, получим
![]() (11.3)
(11.3)
Преобразуем это уравнение:
![]()
т.е.
![]() ,
,
т.е.
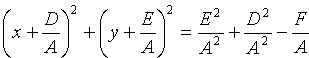 (11.4)
(11.4)
Отсюда следует, что уравнение (11.3) определяет окружность при условии
![]() .
Ее центр находится в точке
.
Ее центр находится в точке
![]() ,
а радиус
,
а радиус
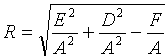 .
.
Если же
![]() ,
то уравнение (11.3) имеет вид
,
то уравнение (11.3) имеет вид
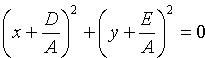 .
.
Ему удовлетворяют координаты единственой точки
![]() .
В этом случае говорят : “окружность выродилась в точку” (имеет нулевой радиус).
.
В этом случае говорят : “окружность выродилась в точку” (имеет нулевой радиус).
Если
![]() ,
то уравнение (11.4), а следовательно, и равносильное уравнение (11.3), не
определят никакой линии, так как правая часть уравнения (11.4) отрицательна, а
левая – не отрицательная (говорять: “окружность мнимая” ).
,
то уравнение (11.4), а следовательно, и равносильное уравнение (11.3), не
определят никакой линии, так как правая часть уравнения (11.4) отрицательна, а
левая – не отрицательная (говорять: “окружность мнимая” ).
Каноническое уравнение эллипса
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
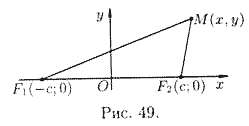 Обозначим
фокусы через F1 и F2, расстояние между ними
через 2c, а сумму расстояний от произвольной точки эллипса до фокусов —
через 2a (см. рис. 49). По определению 2a > 2c, т. е. a
> c.
Обозначим
фокусы через F1 и F2, расстояние между ними
через 2c, а сумму расстояний от произвольной точки эллипса до фокусов —
через 2a (см. рис. 49). По определению 2a > 2c, т. е. a
> c.
Для вывода уравнения эллипса выберем систему координат
![]() так, чтобы
фокусы F1 и F2 лежали на оси
так, чтобы
фокусы F1 и F2 лежали на оси
![]() , а начало
координат совпадало с серединой отрезка F1F2.
Тогда фокусы будут иметь следующие координаты:
, а начало
координат совпадало с серединой отрезка F1F2.
Тогда фокусы будут иметь следующие координаты:
![]() и
и
![]() .
.
Пусть ![]() —
произвольная точка эллипса. Тогда, согласно определению эллипса,
—
произвольная точка эллипса. Тогда, согласно определению эллипса,
![]() , т. е.
, т. е.
![]() (11.5)
(11.5)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим образом:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так как a>с, то
![]() . Положим
. Положим
![]() (11.6)
(11.6)
Тогда последнее уравнение примет вид
![]() или
или
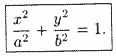 (11.7)
(11.7)
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническимуравнением эллипса.
Эллипс — кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит х и у только в четных степенях, поэтому если
точка ![]() принадлежит
эллипсу, то ему также принадлежат точки
принадлежит
эллипсу, то ему также принадлежат точки
![]() ,
,![]() ,
,![]() .
Отсюда следует, что эллипс симметричен относительно осей
.
Отсюда следует, что эллипс симметричен относительно осей
![]() и
и
![]() , а также
относительно точки
, а также
относительно точки ![]() ,
которую называют центром эллипса.
,
которую называют центром эллипса.
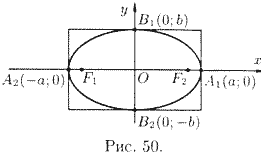 2.
Найдем точки пересечения эллипса с осями координат. Положив
2.
Найдем точки пересечения эллипса с осями координат. Положив
![]() , находим две точки
, находим две точки
![]() и
и
![]() , в которых ось
, в которых ось
![]() пересекает
эллипс (см. рис. 50). Положив в уравнении (11.7)
пересекает
эллипс (см. рис. 50). Положив в уравнении (11.7)
![]() , находим точки
пересечения эллипса с осью
, находим точки
пересечения эллипса с осью
![]() :
:
![]() и
и
![]() . Точки A1,
A2 , B1, B2 называются
вершинами эллипса . Отрезки A1A2 и B1B2,
а также их длины 2a и 2b называются соответственно большой и
малой осями эллипса. Числа a и b называются соответственно
большой и малой полуосями эллипса.
. Точки A1,
A2 , B1, B2 называются
вершинами эллипса . Отрезки A1A2 и B1B2,
а также их длины 2a и 2b называются соответственно большой и
малой осями эллипса. Числа a и b называются соответственно
большой и малой полуосями эллипса.
3. Из уравнения (11.7) следует, что
каждое слагаемое в левой части не превосходит единицы, т.е. имеют место
неравенства
![]() и
и
![]() или
или
![]() и
и
![]() . Следовательно,
все точки эллипса .лежаї внутри прямоугольника, образованного прямыми
. Следовательно,
все точки эллипса .лежаї внутри прямоугольника, образованного прямыми
![]() .
.
4. В уравнении (11.7) сумма неотрицательных слагаемых
![]() и
и
![]() равна
единице. Следовательно, при возрастании одного слагаемого другое будет
уменьшаться, т. е. если
равна
единице. Следовательно, при возрастании одного слагаемого другое будет
уменьшаться, т. е. если
![]() возрастает,
то
возрастает,
то ![]() уменьшается
и наоборот.
уменьшается
и наоборот.
Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
Дополнительные сведения об эллипсе
Форма эллипса зависит от отношения
![]() .
При
.
При ![]() эллипс
превращается в окружность, уравнение эллипса (11.7) принимает вид
эллипс
превращается в окружность, уравнение эллипса (11.7) принимает вид
![]() . В качестве
характеристики формы эллипса чаще пользуются отношением
. В качестве
характеристики формы эллипса чаще пользуются отношением
![]() .
Отношение
.
Отношение
![]() половины
расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом
эллипса и o6oзначается буквой ε («эпсилон»):
половины
расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом
эллипса и o6oзначается буквой ε («эпсилон»):
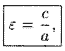 (11.8)
(11.8)
причем 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу (11.8) можно переписать в виде
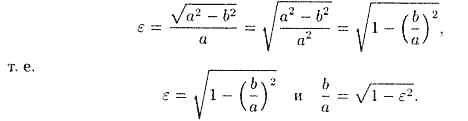
Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.
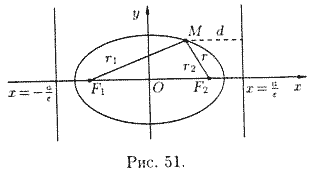 Пусть
М(х;у) -- произвольная точка эллипса с фокусами F1 и F2
(см. рис. 51). Длины отрезков F1M=r1 и F2M = r2
называются фокальными радиусами точки Μ. Очевидно,
Пусть
М(х;у) -- произвольная точка эллипса с фокусами F1 и F2
(см. рис. 51). Длины отрезков F1M=r1 и F2M = r2
называются фокальными радиусами точки Μ. Очевидно,![]()
Имеют место формулы
![]() и
и
![]()
 Теорема
11.1. Если
Теорема
11.1. Если
![]() — расстояние от
произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же
точки до соответствующей этому фокусу директрисы, то отношение
— расстояние от
произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же
точки до соответствующей этому фокусу директрисы, то отношение
![]() есть
постоянная величина, равная эксцентриситету эллипса:
есть
постоянная величина, равная эксцентриситету эллипса:
![]()
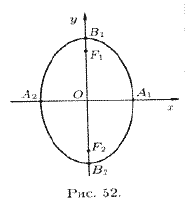
Из равенства (11.6) следует, что
![]() . Если же
. Если же
![]() , то уравнение
(11.7) определяет эллипс, большая ось которого
, то уравнение
(11.7) определяет эллипс, большая ось которого
![]() лежит на оси Оу,
а малая ось
лежит на оси Оу,
а малая ось ![]() — на
оси Ох (см. рис. 52). Фокусы такого эллипса находятся в точках
— на
оси Ох (см. рис. 52). Фокусы такого эллипса находятся в точках
![]() и
и
![]() , где
, где
![]() .
.