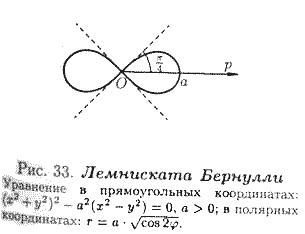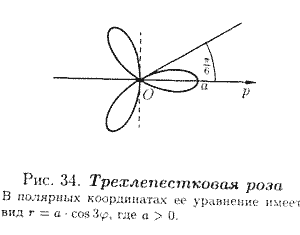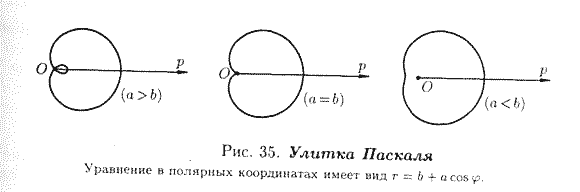Ссылки
§ 9 Система координат на плоскости
Основные понятия
Основные приложения метода
координат на плоскости
Преобразование системы
координат
§ 10 Линии на плоскости
Основные понятия
9.0 СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат.
 Прямоугольная
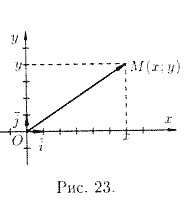
система координат задается двумя взаимно перпендикулярными прямыми — осями, на
каждой из которых выбрано положительное направление и задан единичный
(масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей.
Эти оси называют осями координат, точку их пересечения О - началом координат.
Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу)
(рис. 23).
Прямоугольная
система координат задается двумя взаимно перпендикулярными прямыми — осями, на
каждой из которых выбрано положительное направление и задан единичный
(масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей.
Эти оси называют осями координат, точку их пересечения О - началом координат.
Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу)
(рис. 23).
На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат - вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).
Единичные векторы осей обозначают i и
j(| i |=|
j |=1,
![]() ).
Систему координат обозначают Оху, а плоскость, в которой расположена
).
Систему координат обозначают Оху, а плоскость, в которой расположена
система координат, называют координатной плоскостью.
Рассмотрим произвольную точку Μ плоскости Оху. Вектор ОМ называется радиусом-вектором точки М.
Координатами точки Μ в системе координат Оху называются координаты радиуса-вектора OM. Если OM=(x;y), то координаты точки Μ записывают так: М(х;у), число x называется абсциссой точки М, у — ординатой точки Μ.
Эти два числа x и y полностью определяют положение точки на плоскости, а именно: каждой паре чисел x и y соответствует единственная точка М плоскости, и наоборот.
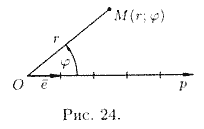
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор.
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
Числа r и φ называются полярными координатами точки М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.
Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (—p; p] (или 0< φ < 2pr), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.
Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
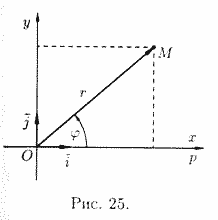
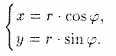
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами
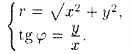
Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что -p < φ< p.
9.2. Основные приложения метода координат на плоскости
Расстояние между двумя точками
Требуется найти расстояние d между точками A(x1;y1) и В(х2;y2) плоскости Оху.
Решение: Искомое расстояние d равно длине вектора
![]() , т.е.
, т.е.
![]()
Деление отрезка в данном отношении
Требуется разделить отрезок АВ, соединяющий точки A(x1;y1)
и В(х2;y2) в заданном отношении λ > 0, т.е. найти
координаты точки М(х;у) отрезка АВ такой, что
![]() (см.
рис. 26).
(см.
рис. 26).
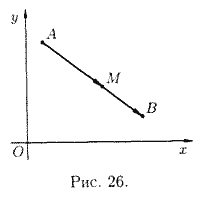 Решение:
Введем в рассмотрение векторы
Решение:
Введем в рассмотрение векторы
![]() и
и![]() .
Точка Μ делит отрезок АВ в отношении λ, если
.
Точка Μ делит отрезок АВ в отношении λ, если
![]() (9.1)
(9.1)
Но![]() , т. е.
, т. е.
![]() и
и
![]() , т. е.
, т. е.
![]() .
.
Уравнение (9.1) принимает вид
![]()
Учитывая, что равные векторы имеют равные координаты, получаем
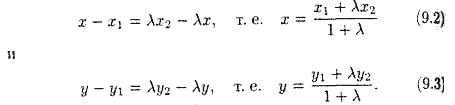
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении. В частности, при λ = 1, т.е. если AM = MB, то они примут вид
![]() ,
,
![]() .
В этом случае точка М(х;у) является
серединой отрезка АВ.
.
В этом случае точка М(х;у) является
серединой отрезка АВ.
Замечание: Если λ = 0, то это означает, что точки A и Μ совпадают,
если λ < 0, то точка Μ лежит вне отрезка АВ — говорят, что точка M делит
отрезок АВ внешним образом (![]() ,
т. к. в противном случае
,
т. к. в противном случае
![]() , т. е. AM + MB
= 0, т. е. АВ = 0).
, т. е. AM + MB
= 0, т. е. АВ = 0).
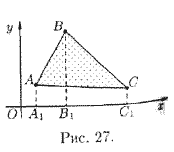
Площадь треугольника
 Требуется
найти площадь треугольника ABC с вершинами А(x1;y1),
В(х2,y2), С(x3;y3).
Требуется
найти площадь треугольника ABC с вершинами А(x1;y1),
В(х2,y2), С(x3;y3).
Решение: Опустим из вершин А, В, С перпендикуляры АА1, ВВ1, СС1 на ось Ох (см. рис. 27).
Очевидно, что
![]()
Поэтому
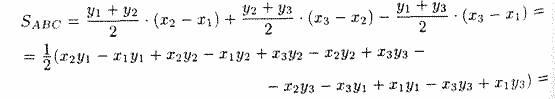
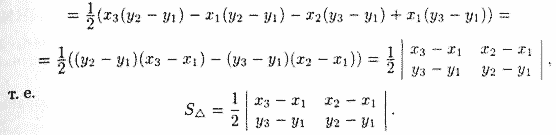
Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
9.3. Преобразование системы координат.
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
Параллельный перенос осей координат
Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от системы координат Оху к новой системе О1х1у1, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными.
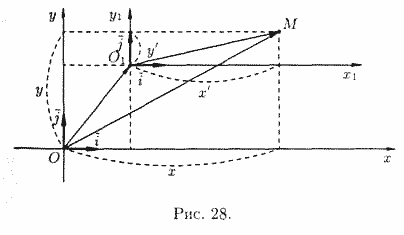
Пусть начало новой системы координат точка О1 имеет координаты (х0;y0) в старой системе координат Оху, т. е. О1 (х0;y0). Обозначим координаты произвольной точки Μ плоскости в системе Оху через (х;у), а в новой системе O1x1y1 через (х';у') (см. рис. 28).
Рассмотрим векторы
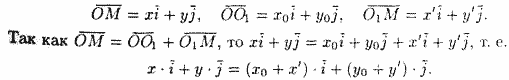
Следовательно,
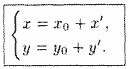
Полученные формулы позволяют находить старые координаты x и у по известным новым х' и у' и наоборот.
Поворот осей координат
 Под
поворотом осей координат понимают такое преобразование координат, при
котором обе оси поворачиваются на один и тот же угол, а начало координат и
масштаб остаются неизменными.
Под
поворотом осей координат понимают такое преобразование координат, при
котором обе оси поворачиваются на один и тот же угол, а начало координат и
масштаб остаются неизменными.
Пусть новая система O1x1y1 получена поворотом системы Оху на угол α.
Пусть Μ произвольная точка плоскости, (х;у) — ее координаты в старой системе и (х';у') — в новой системе.
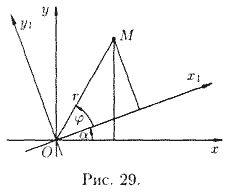
Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Οx1 (масштаб одинаков). Полярный радиус r в обеих системах одинаков, а полярные углы соответственно равны α + j и φ, где φ — полярный угол в новой полярной системе.
По формулам перехода от полярных координат к прямоугольным имеем
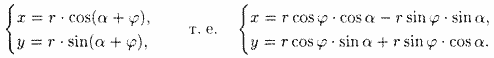
Но rcosj = х' и rsinφ = у'. Поэтому
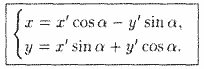
Полученные формулы называются формулами поворота осей. Они позволяют определять старые координаты (х; у) произвольной точки Μ через новые координаты (х';у') этой же точки М, и наоборот.
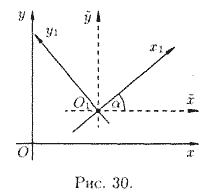 Если
новая система координат O1x1y1 получена из
старой Оху путем параллельного переноса осей координат и последующим поворотом
осей на угол α (см. рис. 30), то путем введения вспомогательной системы
Если
новая система координат O1x1y1 получена из
старой Оху путем параллельного переноса осей координат и последующим поворотом
осей на угол α (см. рис. 30), то путем введения вспомогательной системы
![]() легко
получить формулы
легко
получить формулы
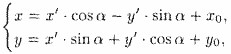
выражающие старые координаты х и у произвольной точки через ее новые координаты х' и у'.
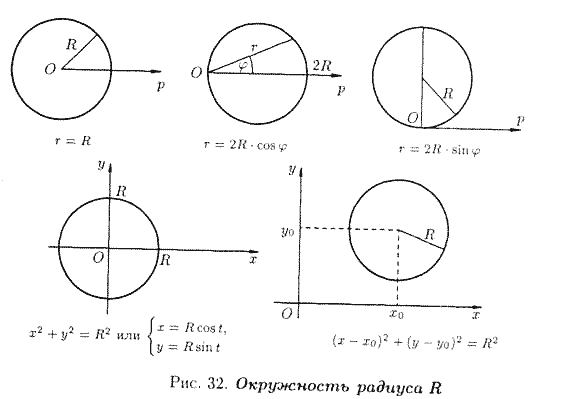
Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние - R от некоторой фиксированной точки О (центра окружности).
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии на плоскости определять с помощью уравнения (т. е. равенства, связывающего координаты точек линии).
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Переменные x и у в уравнении линии называются текущими координатами точек линии.
Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.
Так, для того чтобы установить лежит ли точка А(x0; у0) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбранной системе координат.
Задача о нахождении точек пересечения двух линий, заданных уравнениями F1(x1;y1) = 0 и F2(x2;y} = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:
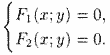
Если эта система не имеет действительных решений, то линии не пересекаются.
Аналогичным образом вводится понятие уравнения линии в полярной системе координат.
Уравнение F(r; φ)=О называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
Линию на плоскости можно задать при помощи двух уравнений:
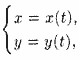 (10.1)
(10.1)
где x и у — координаты произвольной точки М(х; у), лежащей на данной линии, а t — переменная, называемая параметром; параметр t определяет положение точки (х; у) на плоскости.
Например, если x = t + 1, у = t2, то значению параметра t = 1 соответствует на плоскости точка (3; 4), т. к. x = 1 + 1 = 3, у = 22 - 4.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (10.1) — параметрическими уравнениями линии.
Чтобы перейти от параметрических уравнений линии к уравнению вида F(x;y) = 0, надо каким-либо способом из двух уравнений исключить параметр t.
Например, от уравнений
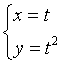 путем
подстановки t = х
путем
подстановки t = х
во второе уравнение, легко получить уравнение у = х2; или у-х2 = 0, т. е. вида F(x; у) = 0. Однако, заметим, такой переход не всегда возможен.
 Линию
на плоскости можно задать векторным уравнением
r=r(t), где t —
скалярный переменный параметр. Каждому значению t0 соответствует
определенный вектор r=r(t) плоскости.
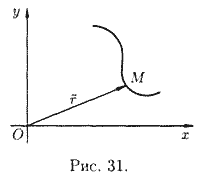
При изменении параметра t конец вектора r=r(t) опишет
некоторую линию (см. рис. 31).
Линию
на плоскости можно задать векторным уравнением
r=r(t), где t —
скалярный переменный параметр. Каждому значению t0 соответствует
определенный вектор r=r(t) плоскости.
При изменении параметра t конец вектора r=r(t) опишет
некоторую линию (см. рис. 31).
Векторному уравнению линии r=r(t) в системе координат Оху соответствуют два скалярных уравнения (10.1), т. е. уравнения проекций на оси координат векторного уравнения линии есть ее параметрические уравнения. I Векторное уравнение и параметрические уравнения I линии имеют механический смысл. Если точка перемеща- I ется на плоскости, то указанные уравнения называются уравнениями движения, а линия — траекторией точки, параметр t при этом есть время. Итак, всякой линии на плоскости соответствует некоторое уравнение вида F(x; у) = 0.
Всякому уравнению вида F(x; у) = 0 соответствует, вообще говоря, некоторая линия, свойства которой определяются данным уравнением (выражение «вообще говоря» означает, что сказанное допускает исключения. Так, уравнению (х-2)2+(у-3)2 =0 соответствует не линия, а точка (2; 3); уравнению х2 + у2 + 5 = 0 на плоскости не соответствует никакой геометрический образ).
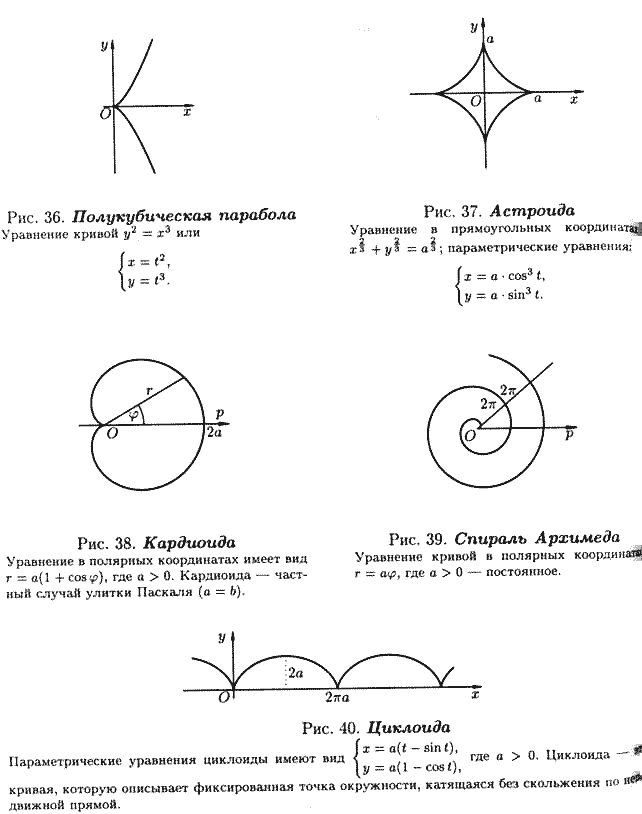
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение) вторая: зная уравнение кривой, изучить ее форму и свойства.
На рисунках 32-40 приведены примеры некоторых кривых и указаны их уравнения.